Author’s Note
Recently I’ve started exploring AI more despite previous reluctance to do so. The main reason being that the people doing AI here at UCLA are very cracked and seem to actually know their stuff.
As a result, I started self-studying Andrew Ng’s course on deep learning & neural networks. So far, I’ve finished the first 2 courses out of 5, which focus on explaining the mathematical models of neural networks and various optimization techniques.
Following Paul Graham’s advice of writing on “topics that you don’t know”, the main goal of this essay is to summarize what I’ve learned so far. The essay will be presented in terms of Q&A’s, as many of these questions are actual questions that I had before.
Neural Network, the Big Picture
Joey: Neural network seems so intimidating! Can you give me a big picture of what neural networks are like?
Chandler: Sure thing! Personally, I think neural network boils down to an optimization problem that seeks to find the optimal parameters that would minimize a mathematical equation. Then it uses those parameters to make predictions.
Joey: Interesting. What do you mean by optimization, parameters, and mathematical equation?
Chandler: Great question. These 3 keywords correspond to 3 key components/steps of a neural network. More specifically,
- Parameters $\longleftrightarrow$ neurons
- Used in forward propagation
- Mathematical equation $\longleftrightarrow$ cost function
- Used to compute cost
- Optimization $\longleftrightarrow$ gradient descent (and its improvements)
- Used in backward propagation
Joey: Wow, that’s cool. I’ve heard of some terms before from linear regression and logistic regression. What distinguishes neural networks from a simple linear regression model?
Chandler: The difference isn’t that big! The main difference comes down to parameters. Whereas a simple logistic regression model will have one set of parameters $W$ and $b$ that we try to optimize, a neural network will contain multiple layers, with layer $l$ containing a $W^{[l]}$ and $b^{[l]}$ that we seek to optimize.
Joey: Hmmm, so neural networks are more complex and have more parameters that we try to optimize. Why do we need multiple layers though? Can’t we put all the parameters into one larger layer?
Chandler: Theoretically, yes. However, “the one larger layer” will need to have exponentially more neurons since a lot of problems are not linearly separable. That’s why a multi-layer neural network works better in solving those problems.
Joey: Ah, now I understand! Can you now go over the three key terms that you mentioned earlier?
Chandler: Absolutely. Let’s talk about forward propagation first.
Forward Propagation
Chandler: Forward propagation is the process of using the current parameters to make a prediction. More specifically, for the $i^{th}$ layer of our neural network, we will call ours parameters $W^{[i]}$ and $b^{[i]}$. Note that $W^{[i]}$ is a $n_i \times n_{i - 1}$ matrix, $b^{[i]}$ is a $n_i \times 1$ vector, with $n_i$ being the number of neurons in the $i^{th}$ layer.
Joey: Cool. How do we make a prediction based on our parameters?
Chandler: For each layer, we will take the previous layer’s output and go through a process called activation, in order to produce the output of the current layer. The output of the very last layer is of course our final prediction.
Joey: Can you be more specific? Also, what’s the activation thing that you just mentioned?
Chandler: Yep! Let’s call the output of the $i^{th}$ layer $A^{[i]}$, which will be a $n_i \times m$ matrix, where $m$ is the batch size, or the number of training examples. Using the output of the previous layer, we can compute the following: \(Z^{[i]} = W^{[i]} {A^{[i - 1]}} + b^{[i]} ,\) \(A^{[i]} = g^{[i]}(Z^{[i]}).\) In the first equation, we compute an intermediate matrix $Z^{[i]}$ using our parameters. Note that in a way, this is a generalized version of the equation of a line $y = mx + b$, with $m$ and $b$ being the parameters in that case. In the second equation, $g^{[i]}$ is the activation function for the $i^{th}$ layer, and we use that to compute $A^{[i]}$, the output of this layer.
Joey: Oh wow, the equations seem complicated, but I think I have a good idea of what they are doing. But why do we need the activation function?
Chandler: Excellent question! Activation functions are there to introduce non-linearity into our neural network. On that note, activation functions shouldn’t be linear for that reason?
Joey: Why is non-linearity important?
Chandler: Without non-linearity, our multi-layer neural network becomes a gimmick. The output of the very last layer our network will still be some linear combination of the parameters in the first layer, which essentially reduces our neural network to 1 layer!
Joey: I’ll make sure to choose a non-linear activation function then! On that note, what are some common activation functions?
Chandler: Sure thing, just take a look at the picture below :D We tend to use ReLU/LeakyReLU in most of the layers, while potentially using Tanh/Sigmoid in the last layer. 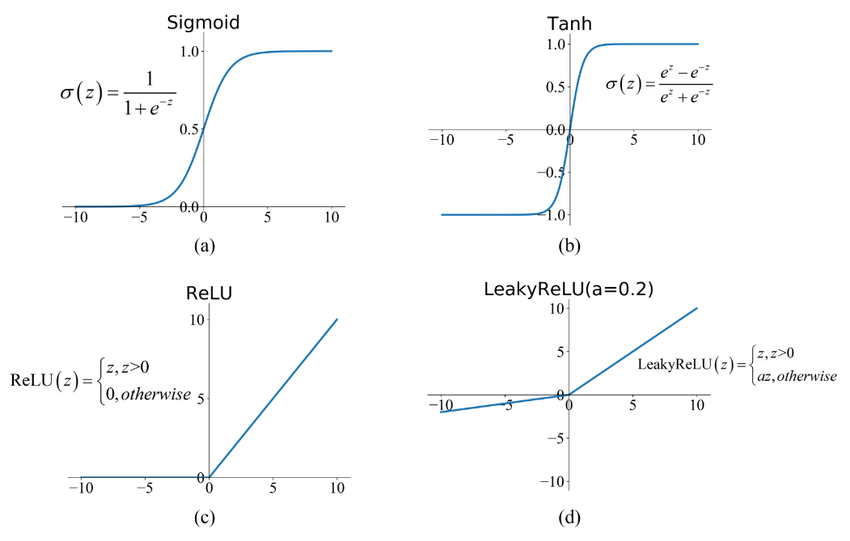
Cost Function
Joey: Wow, I feel like I’ve already learned a lot! Shall we move on to the cost function?
Chandler: Let’s do it! The cost function is actually really easy to understand. Its sole purpose is to assess the prediction our model just made using the current parameters. If the prediction is close, the cost function will return a small value, and vice versa.
Joey: So it’s just like my teachers - giving me a bad grade if my answers are wrong :(
Chandler: You are right, hahaha. Let’s take a look at the specifics of the cost function, or your teacher’s grading rubric. There are many viable options for cost functions, including some very complicated ones, and the choice can impact your model. For example, here is a link to some common ones. For our purposes, two simple cost functions are mean squared error (MSE) and cross-entropy cost.
Back Propagation
Joey: Buneo! Cost function seems pretty easy. You also mentioned that there’s one last step in our model right, what is it again?
Chandler: Yep, the last step is called back propagation. Remember, our goal is to minimize the cost $J$, so the purpose of this step is to update the parameters based on $J$.
Joey: How would you do that?
Chandler: We would use an algorithm called gradient descent. First, let me explain what a gradient is. In mathematics, suppose you have a function $f(x, y, z)$, the gradient $\nabla f = \langle \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \rangle$. The gradient vector points to the (local) minima of $f$, so by “following” the gradient vector, we’d be able to find the minima.
Now, since $J(W, b)$ is a function dependent on the set of parameters $W$ and $b$, we could calculate the gradient of $J$ and update the parameters using that.
Joey: Gradient descent sounds very powerful! How would you calculate it though?
Chandler: Calculating the gradient requires multi-variable calculus. Despite it looking intimidating, if you use the chain-rule and carry out the calculation step by step, it’s actually not so bad! I won’t go into the details here, but you should try to carry out the calculation yourself!
The End + Part 2
Joey: Wow, that’s so interesting! Neural network doesn’t seem as bad as I thought. So are we just done with the model? Would it work well in practice?
Chandler: Yes, we are done with the most basic and fundamental ideas of neural network. However, this is by no means all that there is to neural network - actually, we are not even close. Next time, we are going to talk about optimizations to not only speed up our model, but also make the result more accurate! Stay tune!
 R.I.P. Mathew Perry. Friends and Chandler will forever be special in my heart.
R.I.P. Mathew Perry. Friends and Chandler will forever be special in my heart.